Upper and lower bounds for universal trees

The motivation for studying universal trees comes from parity games. This post does not explain this connection at all, the goal is to present an open problem of purely combinatorial nature
as I hope to appeal to my combinatorially-minded friends.

Definition

We fix two parameters: n, which will be the number of leaves, and h, which will be the height. We look at totally ordered trees with unbounded degree, meaning that each node may have arbitrarily many children and the children of a node are totally ordered. The depth of a node is its distance to the root. For all trees we consider the leaves have the same depth, which is the height of the tree. The size of a tree is its number of leaves.

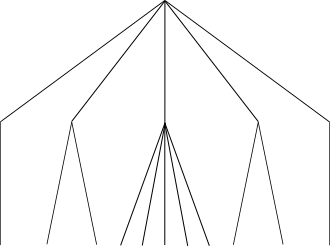
We say that a tree embeds into another if the first one can be obtained by removing nodes from the second. We say that a tree T is (n,h)-universal if all trees of size n and height h embed into T.

An example of a (n,h)-universal tree is the complete tree of height h with each node of degree n. It has size n^h.

Objective: Construct small universal trees

The details for the upper and lower bounds presented in this post can be found in this technical report. A better analysis (of the same constructions) was published in this follow-up paper.

Upper bounds

Theorem:
There exists a (n,h)-universal tree of size f(n,h), where
f(n,h) \le n \binom{\lfloor \log(n) \rfloor + h – 1}{\lfloor \log(n) \rfloor}

A generous upper bound on the expression above is n^{O(\log(h))}. A refined analysis reveals that the expression is polynomial in n and h if h = O(\log(n)).

The construction of Jurdziński and Lazić yields such a tree. We present here a streamlined version, which is marginally better. We construct an (n,h)-universal tree of size f(n,h) by induction, where

f(n,h) = f(n,h-1) + f(\lfloor n/2 \rfloor,h) + f(n – 1 – \lfloor n/2 \rfloor,h)

f(n,1) = n ;\qquad f(h,1) = 1

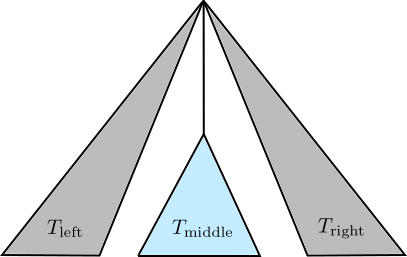
To construct the (n,h)-universal tree T, let:
* T_\text{middle} a (n,h-1)-universal tree;
* T_\text{left} a (\lfloor n/2 \rfloor,h)-universal tree;
* T_\text{right} a (n – 1 – \lfloor n/2 \rfloor,h)-universal tree.

Now construct T as in the drawing above.

We argue that it is (n,h)-universal. Consider a (n,h)-tree t. The question is which part will embed into T_\text{left}, T_\text{middle}, and T_\text{right}. Let v_1,\ldots,v_m be the children of the root of t, and let n(v_i) be the size of the tree rooted in v_i. Choose the unique v_p such that

n(v_1) + \cdots + n(v_{p-1}) \le \lfloor n/2 \rfloor

and

n(v_{p+1}) + \cdots + n(v_m) \le n – 1 – \lfloor n/2 \rfloor.

To embed t into T, proceed inductively
* map v_p to the root of T_\text{middle}
* map the tree obtained by keeping the subtrees rooted in v_1,\ldots,v_{p-1} to T_\text{left}
* map the tree obtained by keeping the subtrees rooted in v_{p+1},\ldots,v_m to T_\text{right}

Lower bounds

Theorem:
Any (n,h)-universal tree has size at least g(n,h), where
g(n,h) \ge \binom{\lfloor \log(n) \rfloor + h – 1}{\lfloor \log(n) \rfloor}

We show by induction that

g(n,h) = \sum_{d = 1}^n g(\lfloor n / d \rfloor,h-1)

g(n,1) = n ;\qquad g(h,1) = 1

Let T be a (n,h)-universal tree, and \delta \in [1,n]. We claim that the number of nodes at depth h-1 of degree greater to or larger than \delta is at least g(\lfloor n / \delta \rfloor,h-1).

Let T_\delta be the subtree of T obtained by
* removing all leaves, and
* removing the nodes at depth h-1 of degree less than \delta in T.
(Note that this can create new leaves, they are recursively removed.)

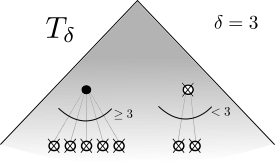
The tree T_\delta has height h-1. We argue that T_\delta is (\lfloor n / \delta \rfloor,h-1)-universal. Indeed, let t be a tree with \lfloor n / \delta \rfloor leaves of height h-1. To each leaf of t we append \delta children, yielding the tree t_+ which has \lfloor n / \delta \rfloor \cdot \delta \le n leaves and height h. Since T is (n,h)-universal, the tree t_+ embeds into T. Observe that the embedding induces an embedding of t into T_\delta, since the leaves of t have degree \delta in t_+, hence are also in T_\delta.

So far we proved that the number of nodes at depth h-1 of degree greater to or larger than \delta is at least g(\lfloor n / \delta \rfloor,h-1). Now, note that the sum over \delta \in [1,n] of the number of nodes at depth h-1 of degree greater to or larger than \delta is a lower bound on the number of leaves, which concludes.

Between lower and upper bounds?

One can show that

\frac{f(n,h)}{g(n,h)} = O(nh)

so there is a (reasonably small but still) gap. The upper bound is tight for h = 2 (there is a bit of work to check this), but I do not know for larger values of h.

Open question: what is the exact size of the smallest (n,h)-universal tree?