Boundedness for (min,plus)-automata

We consider (min,plus)-automata, meaning that an automaton \mathcal{A} computes a function

\mathcal{A} : A^* \to \mathbb{N}_{\infty}

where \mathbb{N}_{\infty} = \mathbb{N} \cup \{\infty\}, by assigning to a word w the minimum value of a run, where the value of a run is computed by summing the weights along the run.

The boundedness problem asks whether the function \mathcal{A} is bounded, meaning

\exists N \in \mathbb{N},\ \forall w \in A^*,\ \mathcal{A}(w) \le N

In this note, we will construct an algebraic structure from an automaton generalising the transition monoid for non-deterministic automata. This algebraic structure is a stabilisation monoid. The answer to the boundedness problem can be found by inspecting the stabilisation monoid: the function \mathcal{A} is bounded if and only if the stabilisation monoid induced by \mathcal{A} does not contain an unbounded witness. The correctness proof of this characterisation relies on a generic tool for stabilisation monoids called Simon’s factorisation theorem.

Extending the transition monoid

Let \mathcal{A} be a (min,plus)-automaton. The transition for letter a is given by

\Delta(a) \in \mathbb{N}_{\infty}^{Q \times Q}

which reads: the cost of going from p to q reading a is \Delta(a)(p,q). Algebraically, we consider the semiring \mathbb{N}_{\infty} with operations \min and +, inducing similar operations on matrices. The function \mathcal{A} : A^* \to \mathbb{N}_{\infty} is defined by \mathcal{A}(w) = I \cdot \Delta(w) \cdot F where I,F \in \mathbb{N}_{\infty}^Q are the initial and final vectors and \Delta is extended to a morphism A^* \to \mathbb{N}_{\infty}^{Q \times Q}.

We also write \mathcal{A}(w)(s,t) for the cost of the minimal run from s to t over the word w.

The special case of non-deterministic automata

Let us consider a special case: \Delta(a) \in \{0,\infty\}^{Q \times Q} and I,F \in \{0,\infty\}^Q. Then \mathcal{A}(w) \in \{0,\infty\}, and \mathcal{A} is essentially a non-deterministic automaton, where \Delta(a)(p,q) = 0 means that there exists a transition from p to q, and \mathcal{A}(w) = 0 if w is accepted. Indeed in algebraic terms the semiring (\{0,\infty\}, \min, +) is isomorphic to the usual boolean semiring (\{0,1\},\vee,\wedge) (where 0 is mapped to 1 and \infty to 0). In this special case, the boundedness problem reduces to the universality problem (note that this implies PSPACE-hardness of the boundedness problem).

We show how to solve the universality problem by computing the transition monoid. The transition monoid \mathcal{M}_\mathcal{A} of a non-deterministic automaton \mathcal{A} is the monoid generated by the matrices \Delta(a) for a \in A. In other words, we start from \{\Delta(a) : a \in A\} and close under matrix product. For the sake of explanation let us see \Delta(a) as a matrix in the boolean semiring (\{0,\infty\}, \min, +). Since \{0,\infty\}^{Q \times Q} is finite, the transition monoid \mathcal{M}_\mathcal{A} is finite and can be effectively computed using a simple saturation algorithm.

One can verify that \mathcal{A} is universal if and only if \mathcal{M}_\mathcal{A} does not contain a matrix M such that I \cdot M \cdot F = \infty. Indeed, the morphism \Delta : A^* \to \mathcal{M}_\mathcal{A} maps words to matrices in \mathcal{M}_\mathcal{A} and a word w is rejected if I \cdot \Delta(w) \cdot F = \infty.

Projecting on a finite semiring

A crucial property for non-deterministic automata is that \{0,\infty\}^{Q \times Q} is finite, implying that the transition monoid is finite, therefore computable. This does not hold anymore for (min,plus)-automata, i.e. in the semiring \mathbb{N}_{\infty}^{Q \times Q}.

The good news is that for answering the boundedness problem it is enough to project \mathbb{N}_{\infty} into a finite semiring. The semiring we are looking at contains three elements: 0,1 and \infty. The intuitive meaning is in terms of costs: 0 is free, 1 is a small cost, and \infty a large cost. We let \pi denote the projection from \mathbb{N}_{\infty} to \{0,1,\infty\}, which simply sends 0 to 0, any finite value to 1 and \infty to \infty.

The two operations are \min and +, with the expected semantics. Using these two operations we can multiply matrices in \{0,1,\infty\}^{Q \times Q}.

Stabilisation

We bring a new operator called stabilisation. Consider the following weighted automaton.

We have \mathcal{A}(a) = 1. The function \mathcal{A} is unbounded, because \mathcal{A}(a^n) = n, diverges for n \to \infty. Hence we need an operator to capture the behaviour of a repeated sequence; the stabilisation operator will do just that!

Define

0^\sharp = 0 \quad 1^\sharp = \infty \quad \infty^\sharp = \infty

At an intuitive level: \sharp corresponds to iterating. Repeating a large number of times an operation with cost 0 yields an operation with cost 0. However, if each operation costs 1, the whole operation becomes very costly.

A matrix M is idempotent if M^2 = M. The stabilisation operator over matrices is defined for idempotent matrices by

M^\sharp(s,t) = \min \left\{ M(s,p) + M(p,p)^\sharp + M(p,t) : p \in Q \right\}

Intuitively: how much does it cost to go from s to t by repeating the action M a large number of times? The path achieving the minimum goes from s to some p, follows a loop around p, and then from p to t, with the whole operation of cost M(s,p) + M(p,p)^\sharp + M(p,t).

We now have a unary operation on (idempotent) matrices. What we have done is defining a stabilisation monoid, which is given by a set (here matrices over \{0,1,\infty\}), a binary operation (multiplication of matrices) and a unary operation called stabilisation.

The stabilisation monoid of a (min,plus)-automaton

Given a (min,plus)-automaton \mathcal{A}, we define its stabilisation monoid \mathcal{M}_\mathcal{A} to be the stabilisation monoid generated by the matrices \pi(\Delta(a)) for a \in A. For convenience we let \mathbf{a} denote \pi(\Delta(a)). In other words, we start from \{\mathbf{a} : a \in A\} and close under matrix product and stabilisation. Since the underlying semiring is finite, the stabilisation monoid is finite and can be effectively computed using a simple saturation algorithm.

We say that a matrix M is an unbounded witness if I \cdot M \cdot F = \infty.

Theorem:
Let \mathcal{A} be a (min,plus)-automaton. \mathcal{A} is bounded if and only if \mathcal{M}_\mathcal{A} does not contain any unbounded witness.

This yields an algorithm for deciding boundedness. A naive implementation is in EXPTIME; a further analysis of the stabilisation monoid gives a PSPACE algorithm.

One direction is easy: let M \in \mathcal{M}_\mathcal{A} be an unbounded witness. One can associate with M a \sharp-expression explaining how M was computed in \mathcal{M}_\mathcal{A}: for instance, ((a^\sharp) b)^\sharp represents the computation:
* first apply the stabilisation operator to \mathbf{a},
* then multiply the result with \mathbf{b},
* finally apply the stabilisation operator to the result.

Following the inductive construction of the \sharp-expression, one can construct a sequence of words (w_n)_{n \in \mathbb{N}} (essentially replacing \sharp by n) such that

\lim_n\ \mathcal{A}(w_n)(p,q) = \infty \text{ if and only if } M(p,q) = \omega

Hence the fact that M is an unbounded witness implies that \lim_n \mathcal{A}(w_n) = \infty.

In the remainder of this post we prove the converse more challenging implication, called completeness.

Simon’s factorisation theorem

Imagine that we have some (min,plus)-automaton \mathcal{A} and we are looking at \mathcal{A}(w) for some word w (which we can think of as very long), for instance (ab)^{300000}. As an approximation let us think of this word as (ab)^n for a very large n.
We want to know whether \mathcal{A}((ab)^n) is large, or in other words whether it diverges to infinity when n \to \infty: this is equivalent to asking whether I \cdot (\mathbf{a} \cdot \mathbf{b})^\sharp \cdot F = \omega.

The word (ab)^{300000} had an obvious factorisation into (ab)^n for a large n. Simon’s factorisation theorem says that any word can be factorised in a similar way. Let us formalise this notion of factorisation. Let \mathcal{M} be a stabilisation monoid and a morphism \phi : A^* \to \mathcal{M}, the factorisation of \phi(w) is a tree such that
* each node is labeled by a pair (M,u) where M \in \mathcal{M} and u \in A^*,
* the leaves are labeled by (\phi(a),a) for a \in A,
* reading the second component of the leaves from left to right yields the word w,
* the internal nodes are of two types: product nodes and stabilisation nodes,
* a product node has two children, let (M_1,w_1) and (M_2,w_2) be their labels, then the label of the node is (M_1 \cdot M_2, w_1 w_2),
* a stabilisation node has k \ge 3 children, let (M,w_i) be their labels, then M is an idempotent of \mathcal{M} (meaning M^2 = M) and the label of the node is (M^\sharp, w_1 \cdots w_k).

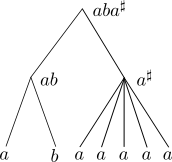
Theorem:
Let \mathcal{M} be a stabilisation monoid and a morphism \phi : A^* \to \mathcal{M}. There exists a constant K such that for all words w \in A^*, there exists a factorisation of \phi(w) of depth K.

The theorem says that no matter of long, complicated and messy a word is, it can be factorised through \phi by a tree of constant depth. Here constant means that the value depends on \mathcal{M} but not on the word. The optimal K is 3|\mathcal{M}|.

Finishing the proof

Let us assume that there are no unbounded witness and prove that \mathcal{A} is bounded.
Consider a word w. Thanks to Simon’s factorisation theorem applied to the morphism
\phi : A^* \to \mathcal{M}_\mathcal{A} defined by \phi(a) = \mathbf{a}, there exists a factorisation of \phi(w) of depth K. We will reason on this tree.

We let W denote the maximal weight appearing in the (min,plus)-automaton \mathcal{A}.

Lemma:
For all nodes labeled (M,u) at distance d from the leaves, for all states s,t we have
M(s,t) = 0 \implies \mathcal{A}(u)(s,t) = 0
M(s,t) = 1 \implies \mathcal{A}(u)(s,t) \le 2^d \cdot W

We prove the lemma by induction from the leaves to the root.
* If the node is a leaf this is by definition of \phi(a) and W.
* If the node is a product node labeled (M_1 M_2,w_1 w_2).
The first item is easy to prove, let us focus on the second. Assume (M_1 M_2)(s,t) = 1, this implies that there exists p such that M_1(s,p) = 1 and M_2(p,t) = 1. It follows by induction hypothesis that \mathcal{A}(u)(s,t) \le \mathcal{A}(u_1)(s,p) + \mathcal{A}(u_2)(p,t) \le 2 \cdot 2^{d-1} \cdot W.
* If the node is a stabilisation node labeled (M^\sharp,w_1 \ldots w_k).
Again we only prove the second item, the first one is easy. Assume (M^\sharp)(s,t) = 1, this implies that there exists p such that M(s,p) + M^\sharp(p,p) + M(p,t) = 1 so M(s,p) = M(p,t) = 1 and M(p,p) = 0. It follows by induction hypothesis that

\mathcal{A}(w_1 \ldots w_k)(s,t) \le \mathcal{A}(w_1)(s,p) + \mathcal{A}(w_2)(p,p) + \cdots + \mathcal{A}(w_{k-1})(p,p) + \mathcal{A}(w_k)(p,t)
which is bounded by 2^{d-1} \cdot W + 0 + 2^{d-1} \cdot W.

We can now finish the proof of completeness. Since \mathcal{M}_\mathcal{A} does not contain any unbounded witness, the previous lemma implies that \mathcal{A}(w) is bounded by 2^K W where K is the constant inherited from Simon’s factorisation theorem.